[Algorithm] 프로그래머스 Lv.1: 기사단원의 무기
🖐🏻 시간초과로 실패한 코드를 시간 복잡도를 줄인 효율적인 코드로 개선해보겠다!
- Level: 1
- Algorithm: 자료구조, 구현
- Language: Python3
1. ⚡️ Problem
약수 개수 구하기
- 숫자 number까지의 모든 숫자에서 약수 개수를 계산하고, 특정 조건에 따라 값을 변경한 후 합을 구하는 문제
2. ⚡️ Solution #1 (기존)
1) 코드
def solution(number, limit, power):
divisor_cnts = []
for num in range(1, number+1): # O(number)
divisor_cnts.append(count_divisors(num))
for idx, div in enumerate(divisor_cnts): # O(number)
if div > limit:
divisor_cnts[idx] = power
ans = sum(divisor_cnts) # O(number)
return ans
def count_divisors(n):
divisors = []
for i in range(1, n+1): # O(n)
if n % i == 0:
divisors.append(i)
return len(divisors)
2) 문제점: 시간 복잡도
📐 약수 계산 원리
count_divisors(num)함수는 약수 개수를 1부터 num까지 모든 숫자로 나누어 약수를 찾는 방식이다.
⏰ 시간 복잡도 분석
- 숫자 num의 약수를 계산하는 함수 count_divisors(num)은 최대 num번 루프를 돈다.
O(num) -
이 작업은 숫자 1부터 number까지 실행되므로, 전체 시간 복잡도는 다음과 같다:
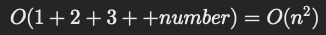
- 예시 계산:
- number = 6 인 경우, 계산 횟수는 다음과 같다.
count_divisors(1) ➔ 1번 count_divisors(2) ➔ 2번 count_divisors(3) ➔ 3번 count_divisors(4) ➔ 4번 count_divisors(5) ➔ 5번 count_divisors(6) ➔ 6번 - 총 계산 횟수 = 1 + 2 + 3 + 4 + 5 + 6 = 21회
-
이 합은 수학적으로 등차수열 합 공식을 통해 계산된다:
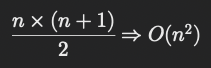
- number = 6 인 경우, 계산 횟수는 다음과 같다.
3. ⚡️ Solution #2 (개선)
1) 코드
def solution(number, limit, power):
divisor_cnts = calculate_divisors_up_to(number)
for idx, div in enumerate(divisor_cnts): # O(number)
if div > limit:
divisor_cnts[idx] = power
ans = sum(divisor_cnts) # O(number)
return ans
def calculate_divisors_up_to(n):
divisor_cnts = [0] * (n + 1)
for i in range(1, n + 1): # O(n)
for j in range(i, n + 1, i): # O(n/i)
divisor_cnts[j] += 1
return divisor_cnts
2) 문제 해결: 시간 복잡도 개선
📐 아이디어: 배수 개념 사용
- 약수를 구하려면 특정 수 i가 어떤 수 num의 약수인지 일일이 확인할 필요가 없다.
-
i가 특정 수 num의 약수라면, num은 “i의 배수” 여야 한다.
- Ex) 2의 배수는 2, 4, 6, …이므로, 이 숫자들은 모두 2를 약수로 가진다.
- 즉, 기존 방식에서 개선 된 방식의 변화를 보면 (number=6이라면),
-
기존:
- 1의 약수: 1 - 2의 약수: 1, 2 - 3의 약수: 1, 3 - 4의 약수: 1, 2, 4 - 5의 약수: 1, 5 - 6의 약수: 1, 2, 3, 6 -
개선:
- 1은 배수 1, 2, 3, 4, 5, 6의 약수 - 2는 배수 2, 4, 6의 약수 - 3은 배수 3, 6의 약수 - 4는 배수 4의 약수 - 5는 배수 5의 약수 - 6은 배수 6의 약수
-
⏰ 시간 복잡도 분석
- 바깥 loop
(for i in range(1, n+1))➔O(n)- i는 1부터 n까지 현재 약수로 확인할 수
- 안쪽 loop
(for j in range(i, n+1, i))➔O(n/i)- 숫자 i의 배수를 찾으므로 n/i 만큼 실행된다.
- Ex) i=2일 때 j=2, 4, 6, …
-
전체 시간 복잡도
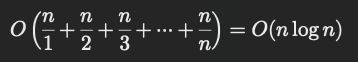
⚡ 4. 결론
| 방법 | 시간 복잡도 | 원리 |
|---|---|---|
| 기존 코드 | O(n²) | 모든 숫자마다 약수를 직접 탐색 |
| 개선 코드 | O(n log n) | 배수 개념을 활용해 약수를 한 번에 계산 |
✔️ 기존 코드 (완전 탐색)
- 숫자 하나하나에 대해 count_divisors(num)을 호출하며 모든 숫자를 다 확인.
-
작은 숫자라도 큰 숫자에서 반복이 많아 매우 비효율적.
- count_divisors(1) ➔ [1] - count_divisors(2) ➔ [1, 2] - count_divisors(3) ➔ [1, 3] - count_divisors(4) ➔ [1, 2, 4] - count_divisors(5) ➔ [1, 5] - count_divisors(6) ➔ [1, 2, 3, 6]
✔️ 개선 코드 (배수 활용)
-
숫자 i의 배수들을 업데이트하므로 훨씬 효율적.
i = 1 ➔ 1의 배수들 업데이트 ➔ [1, 1, 1, 1, 1, 1] i = 2 ➔ 2의 배수들 업데이트 ➔ [1, 2, 1, 2, 1, 2] i = 3 ➔ 3의 배수들 업데이트 ➔ [1, 2, 2, 2, 1, 3] i = 4 ➔ 4의 배수 업데이트 ➔ [1, 2, 2, 3, 1, 3] i = 5 ➔ 5의 배수 업데이트 ➔ [1, 2, 2, 3, 2, 3] i = 6 ➔ 6의 배수 업데이트 ➔ [1, 2, 2, 3, 2, 4]


Leave a comment