[Linear Algebra] Linear combinations, span and basis vectors

1. Basis Vectors (기저벡터)

• xy좌표계에는 2가지 벡터가 존재 (i hat, j hat)
  • i hat: the unit vector in the x-direction
  • j hat: the unit vector in the y-direction
• 좌표쌍이 나타나는 벡터를 두 scaling 된 벡터의 합의 관점으로 보기!
  • 벡터의 x좌표를 i hat을 scaling하는 스칼라로 생각.
  • 벡터의 y좌표를 j hat을 scaling하는 스칼라로 생각.

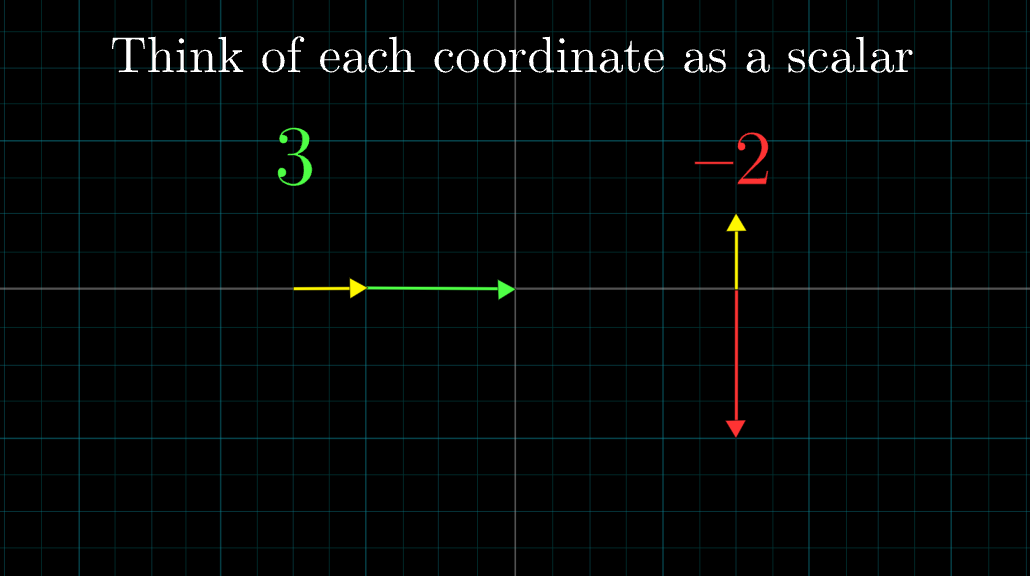
• 기저벡터: i hat, j hat → together they are called the “basis” of the coordinate system

• 완전히 새로운 기저벡터를 선택한다면 새로운 좌표계를 얻을 수도 있다.

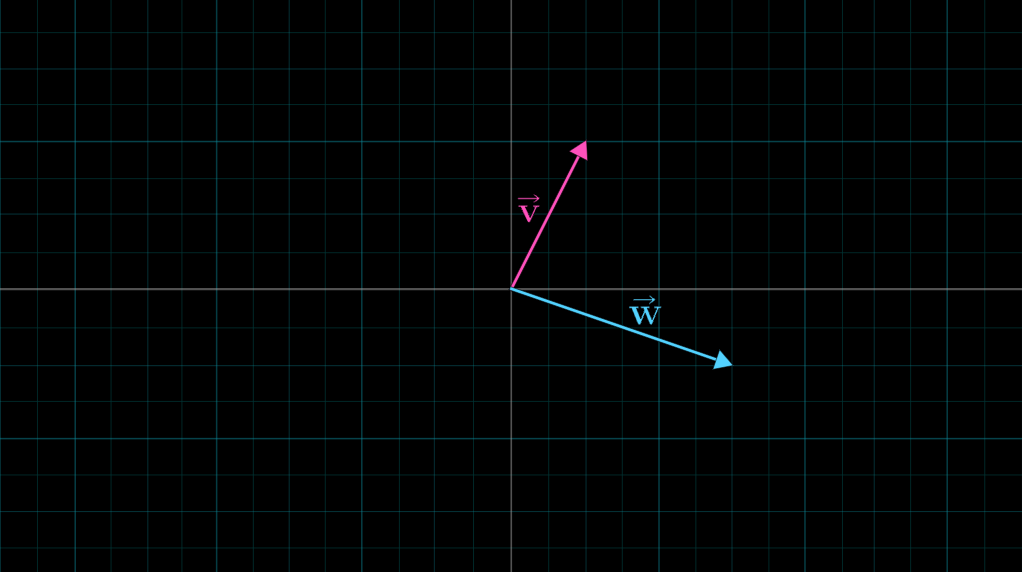
2. Linear Combinations (선형결합)

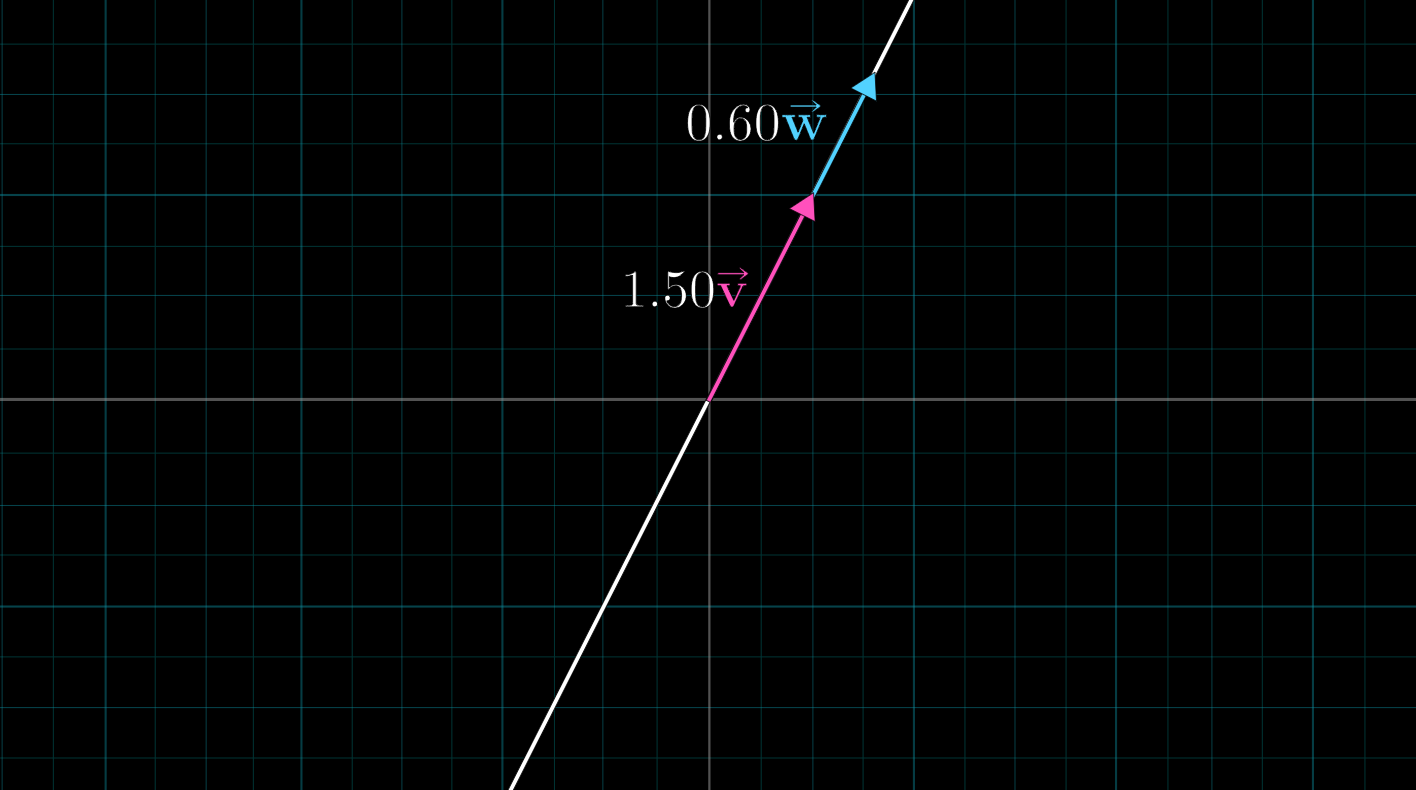
• 두 벡터를 scaling하고 더하여 새로운 벡터를 얻는 연산을 linear combinations(두 벡터의 선형결합)이라 부른다.
• linear 단어는 어디에서 온 것일까?
  • 두 스칼라 중 하나는 고정해놓고 다른 하나의 값을 자유롭게 움직이게 한다면, 두 벡터의 합 벡터의 머리가 한 직선을 그리게 된다.
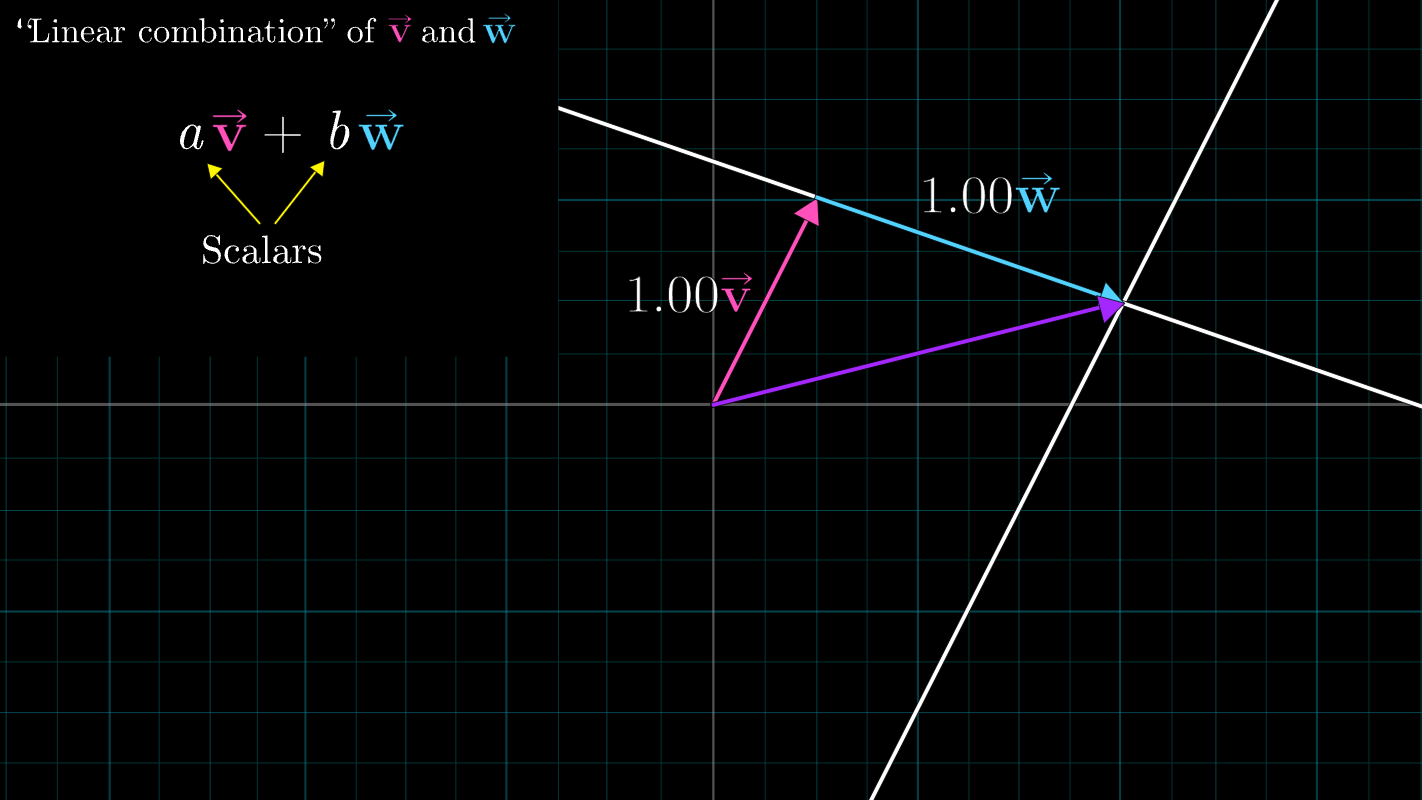
  • 만약 두 스칼라의 범위를 모두 자유롭게 움직이게 한다면,
    • case1) 두 벡터의 합 벡터의 머리가 평면 위 모든 점에 접근이 가능하게 된다. (2차원 공간의 모든 벡터)
    • case2) 두 기저벡터가 같은 직선 상에 위치한 경우에는 두 벡터의 합 벡터가 원점을 지나는 한 직선으로 제한된다.
    • case3) 두 벡터가 모두 영벡터인 경우, 원점에 갇히게 된다.

case2)

case3)

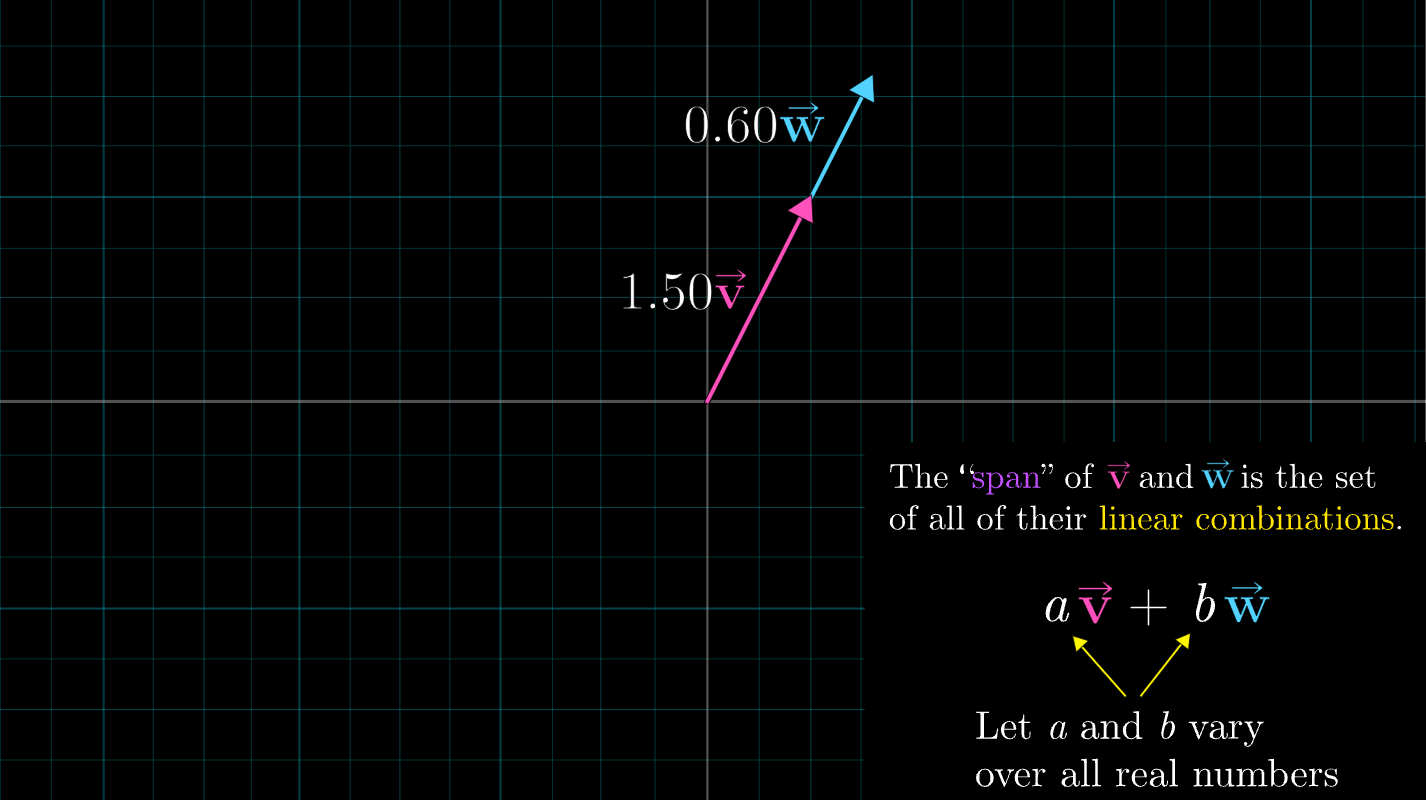
3. Span

• span: 주어진 벡터 쌍의 선형결합으로 만들 수 있는 모든 합 벡터의 집합
• 대부분의 2차원 벡터쌍의 span은 2차원 공간의 벡터 전체가 된다(case1).
• 두 벡터가 일직선 상에 있다면 어떤 직선에 한정되는 모든 벡터가 두 벡터의 span(case2).

4. Vectors vs. Points (벡터와 점)

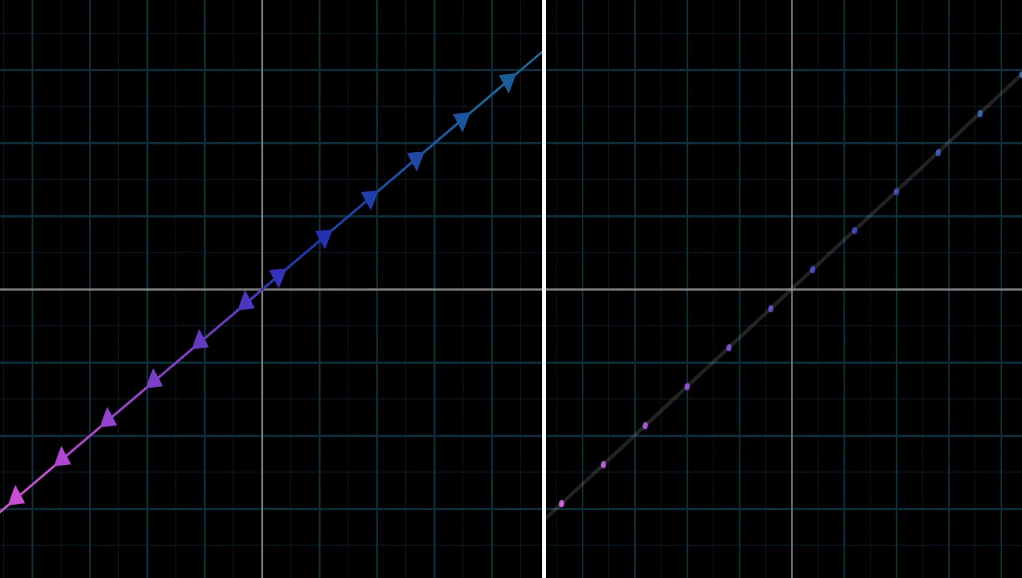
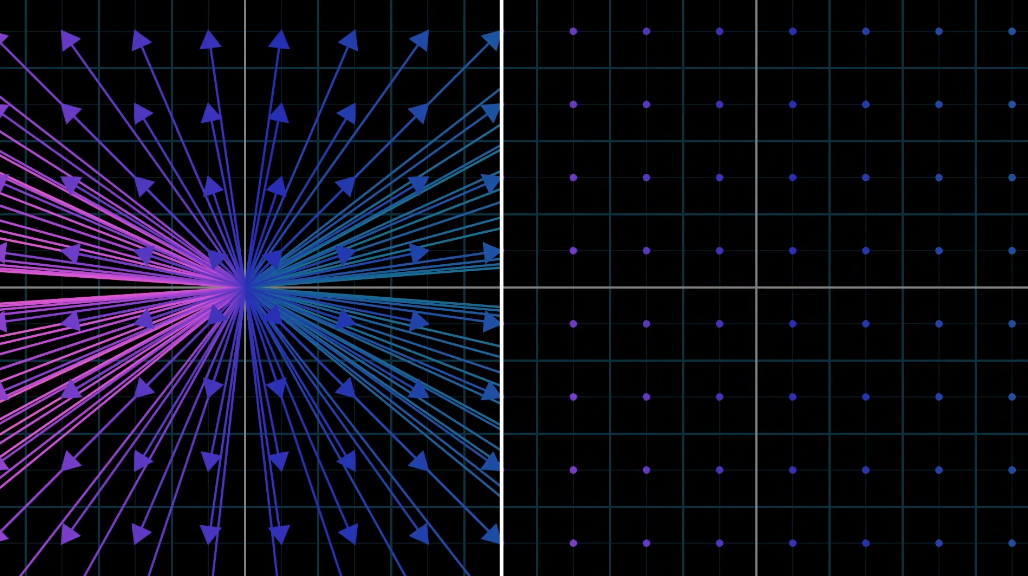
• 좌표평면을 가득 메우는 모든 2차원 벡터를 생각할 때 각각의 벡터를 공간상 점으로 생각하면 편하다.
  • 점의 위치: 벡터의 끝점
  • 원점: 벡터의 시작점
• 이렇게 하면, 한 직선에 나열된 모든 가능한 벡터를 하나의 직선으로 생각할 수 있다.
• 마찬가지로, 모든 가능한 2차원 벡터를 하나의 2차원 평면으로 생각할 수 있다.

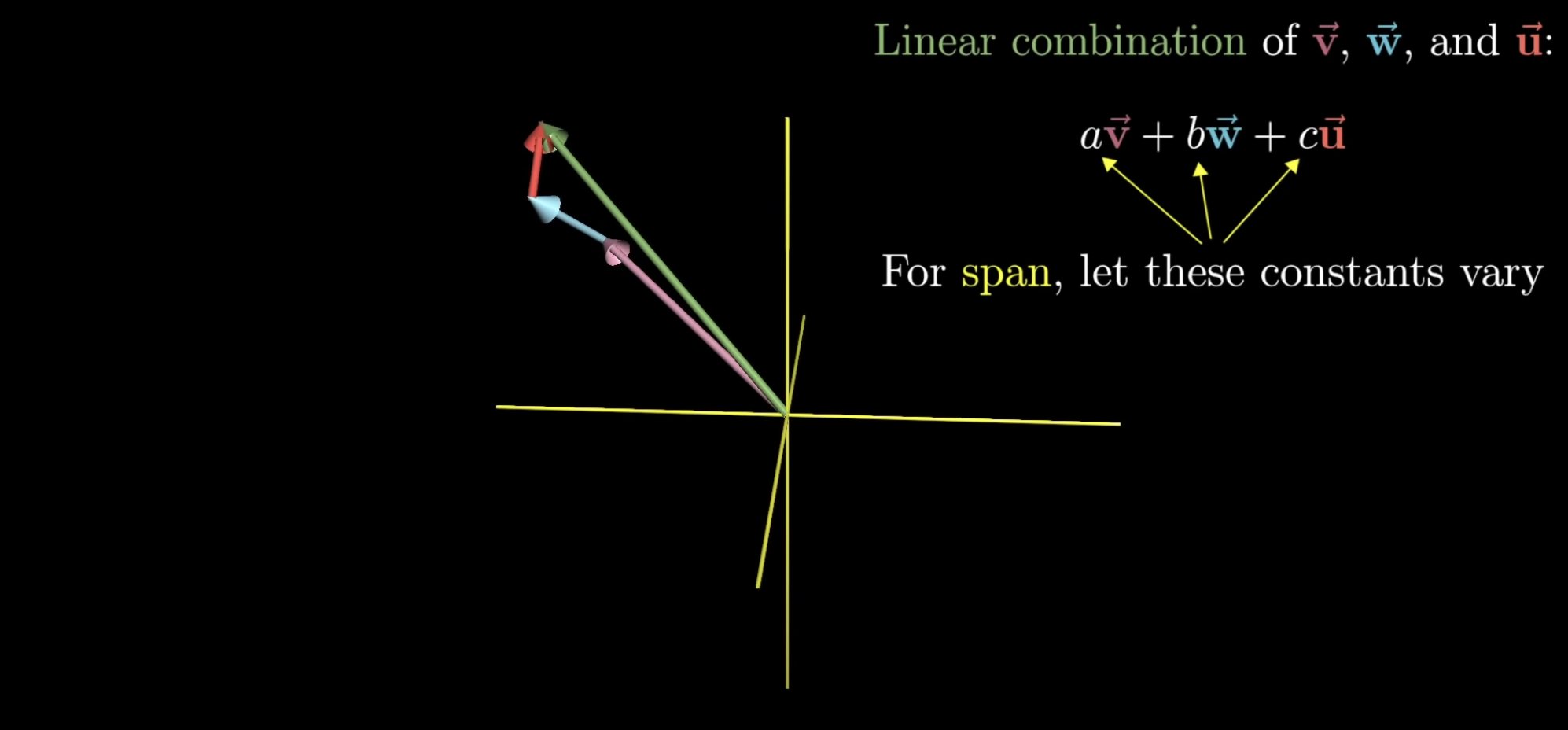
5. Span in 3D

• 이제 3번째 벡터를 더해 3개 벡터의 span을 생각해본다면?
  • 마찬가지로, 3개의 스칼라를 통해 각 벡터를 scaling한 뒤 모두 더하는 것!
  • 이렇게 생성된 결과 벡터들의 span은 모든 가능한 선형결합의 집합.
    • case1) 만약 3번째 벡터가 다른 두 벡터의 span 위에 놓여있다면, span은 변화없이 똑같은 평면을 이룬다. (linearly dependent)
    • case2) 만약 3번째 벡터가 다른 두 벡터의 span 위에 놓여있지 않다면, 결과벡터가 모든 가능한 3차원 벡터에 접근하게 된다. 즉, 두 벡터의 span(평면)이 3번째 벡터를 따라 움직이며 공간 전체를 움직인다.

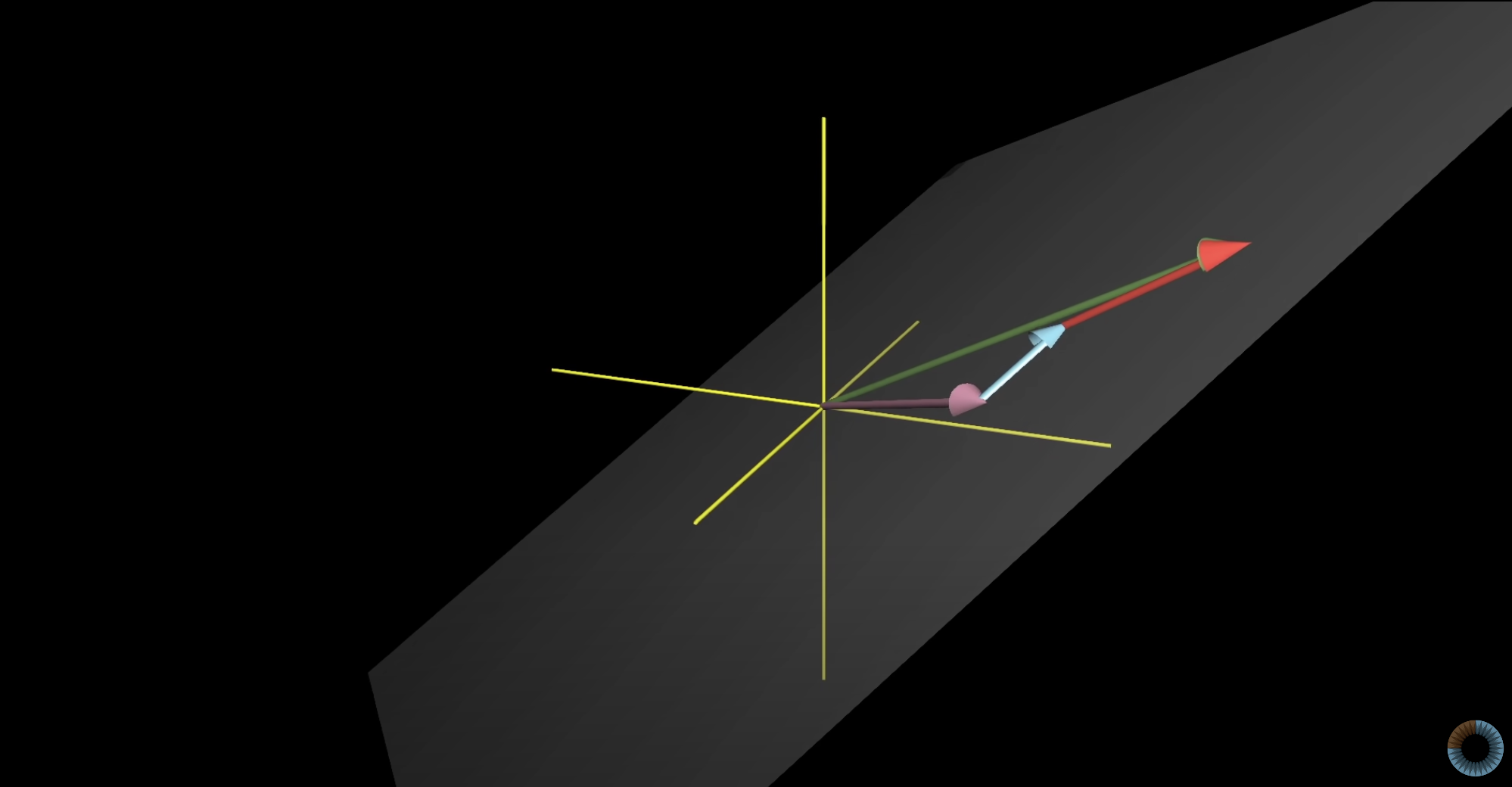case1)

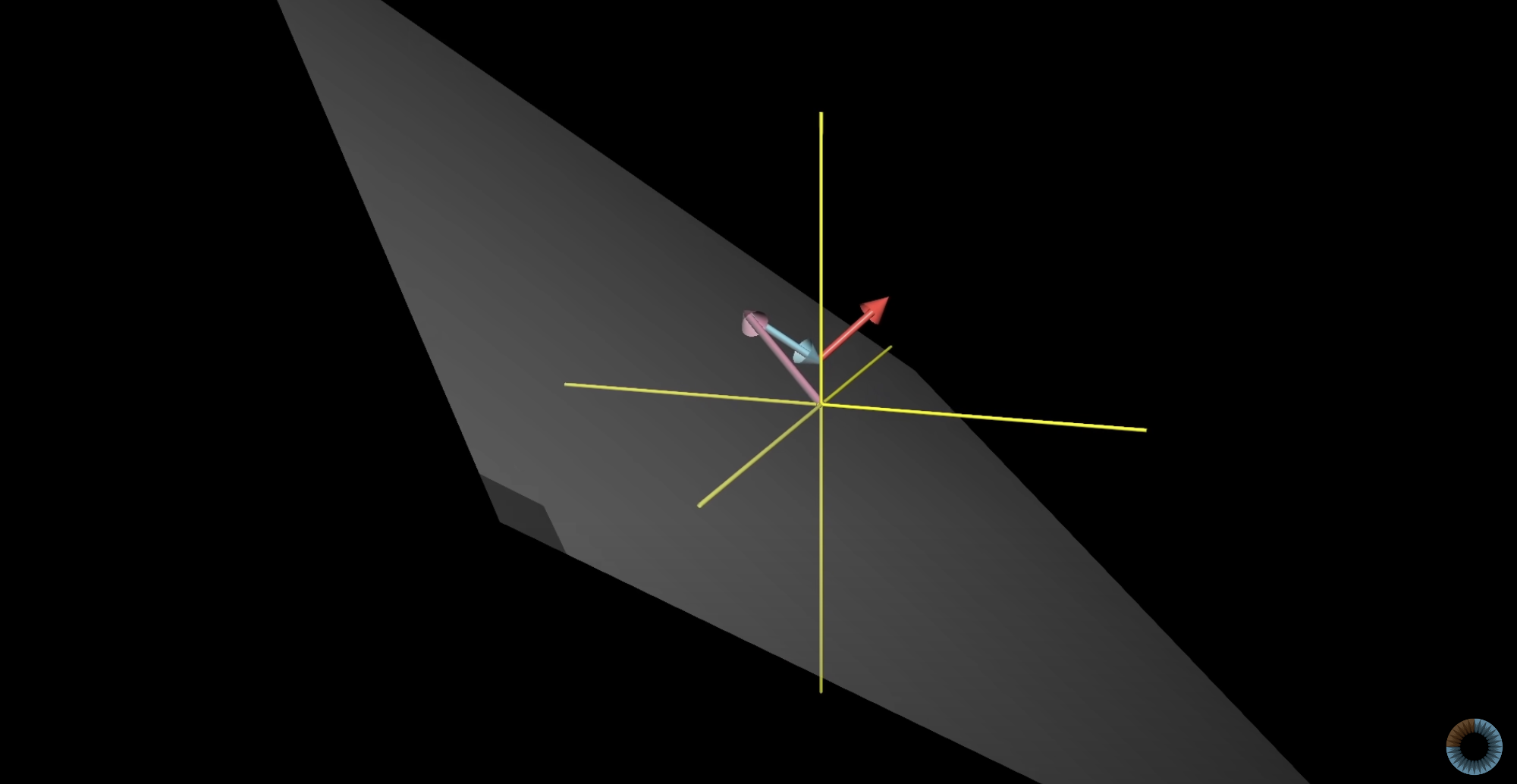case2)

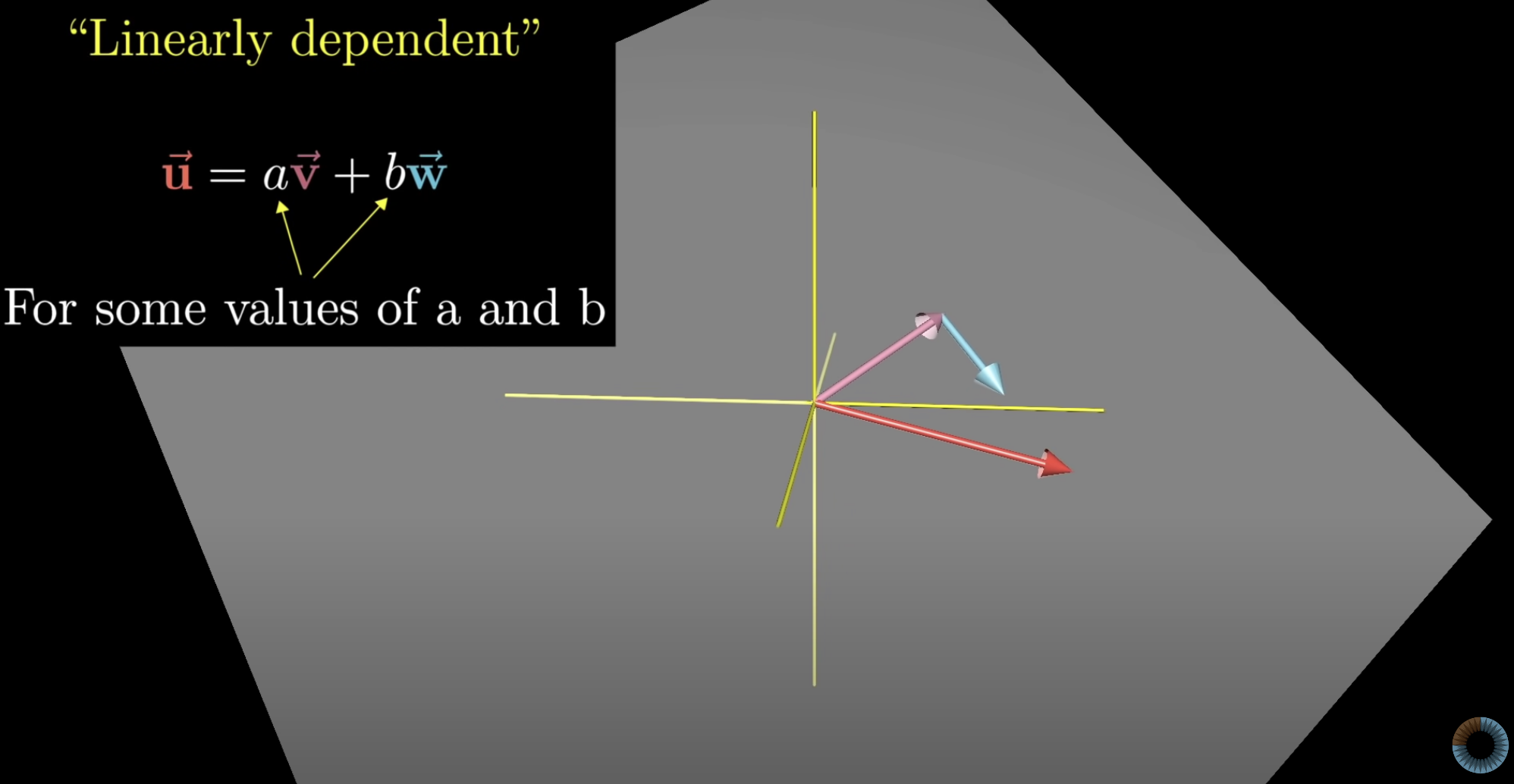
• Linearly dependent (선형종속): 벡터들 중 최소한 하나는 span에 아무런 영향을 끼치지 않아 불필요한 경우, 벡터들이 ‘linearly dependent’하다고 표현. (= 벡터 중 하나가 다른 벡터들의 선형결합으로 표현될 수 있다.)

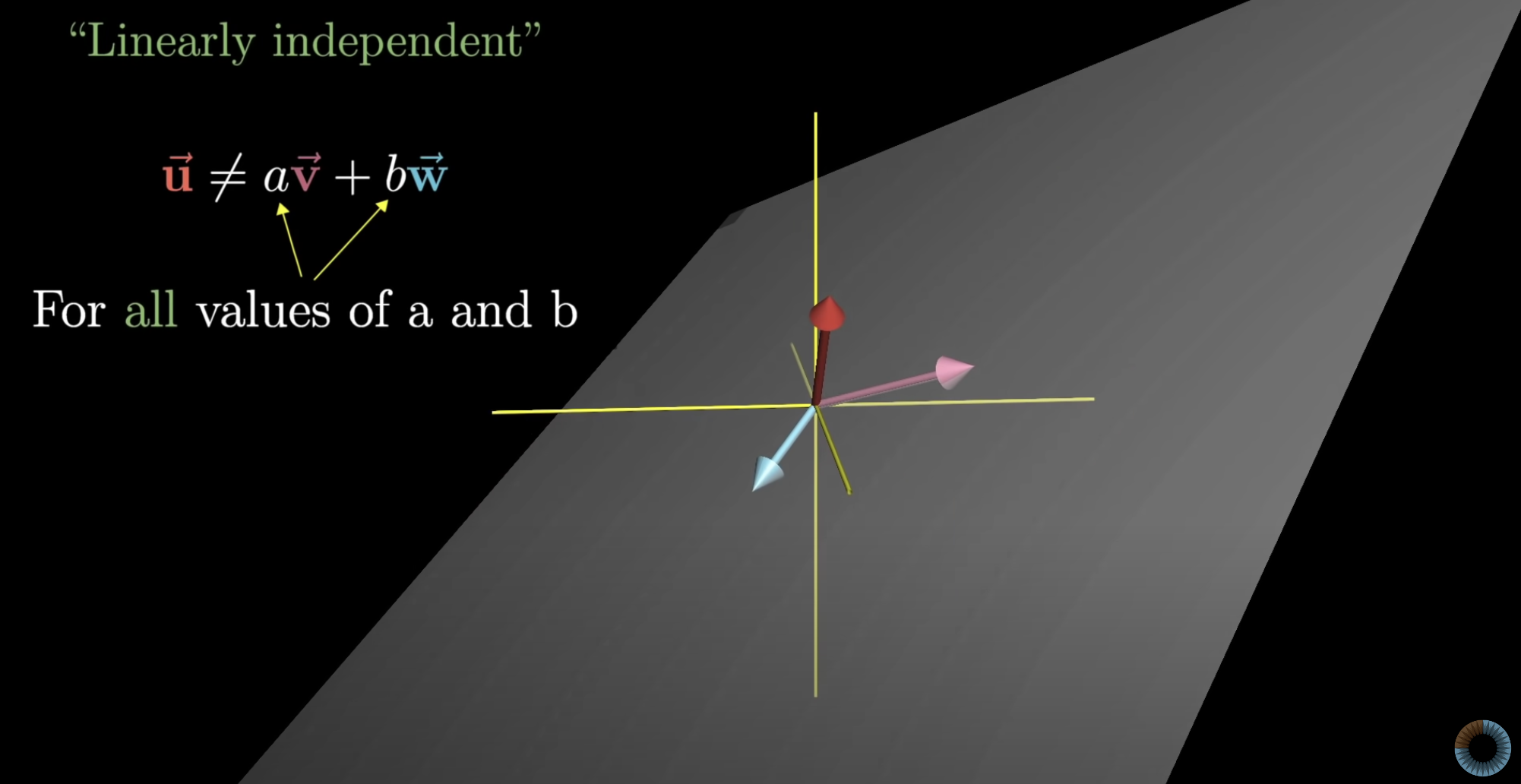
• Linearly independent (선형독립): 모든 벡터가 span에서 각자 다른 차원을 구성하는 경우, 벡터들이 ‘linearly independent’하다고 표현.

Reference

• [3Blue1Brown] Essence of Linear Algebra - Chapter 2